Coxeter–Dynkin diagram
In geometry, a Coxeter–Dynkin diagram (or Coxeter diagram, Coxeter graph) is a graph with numerically labeled edges (called branches) representing the spatial relations between a collection of mirrors (or reflecting hyperplanes). It describes a kaleidoscopic construction: each graph "node" represents a mirror (domain facet) and the label attached to a branch encodes the dihedral angle order between two mirrors (on a domain ridge). An unlabeled branch implicitly represents order-3.
Each diagram represents a Coxeter group, and Coxeter groups are classified by their associated diagrams.
Dynkin diagrams are closely related objects, which differ from Coxeter diagrams in two respects: firstly, branches labeled "4" or greater are directed, while Coxeter diagrams are undirected; secondly, Dynkin diagrams must satisfy an additional (crystallographic) restriction, namely that the only allowed branch labels are 2, 3, 4, and 6. See Dynkin diagrams for details. Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras.[1]
Contents |
Description
Branches of a Coxeter–Dynkin diagram are labeled with a rational number p, representing a dihedral angle of 180°/p. When p = 2 the angle is 90° and the mirrors have no interaction, so the branch can be omitted from the diagram. If a branch is unlabeled, it is assumed to have p = 3, representing an angle of 60°. Two parallel mirrors have a branch marked with "∞". In principle, n mirrors can be represented by a complete graph in which all n(n − 1) / 2 branches are drawn. In practice, nearly all interesting configurations of mirrors include a number of right angles, so the corresponding branches are omitted.
Geometric visualizations
The Coxeter–Dynkin diagram can be seen as a graphic description of the fundamental domain of mirrors. A mirror represents a hyperplane within a given dimensional spherical or Euclidean or hyperbolic space. (In 2D spaces, a mirror is a line, and in 3D a mirror is a plane).
These visualizations show the fundamental domains for 2D and 3D Euclidean groups, and 2D spherical groups. For each the Coxeter diagram can be deduced by identifying the hyperplane mirrors and labelling their connectivity, ignoring 90-degree dihedral angles (order 2).
Coxeter groups in the plane with equivalent diagrams. Domain mirrors are labeled as branch m1, m2, etc. Vertices are colored by their reflection order. The prismatic group 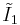 x x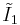 is shown as a doubling of the is shown as a doubling of the 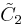 , but can also be created as rectangular domains from doubling the , but can also be created as rectangular domains from doubling the 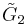 triangles. The triangles. The 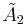 is a doubling of the is a doubling of the 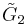 triangle. triangle. |
|
Coxeter groups in 3-space with diagrams. Mirrors (triangle faces) are labeled by opposite vertex 0..3. Branches are colored by their reflection order. 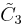 fills 1/48 of the cube. fills 1/48 of the cube. 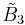 fills 1/24 of the cube. fills 1/24 of the cube. 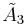 fills 1/12 of the cube. fills 1/12 of the cube. |
Coxeter groups in the sphere with equivalent diagrams. One fundamental domain is outlined in yellow. Domain vertices (and graph branches) are colored by their reflection order. |
Application with uniform polytopes
Coxeter–Dynkin diagrams can explicitly enumerate nearly all classes of uniform polytope and uniform tessellations. Every uniform polytope with pure reflective symmetry (all but a few special cases have pure reflectional symmetry) can be represented by a Coxeter–Dynkin diagram with permutations of markups. Each uniform polytope can be generated using such mirrors and a single generator point: mirror images create new points as reflections, then polytope edges can be defined between points and a mirror image point. Faces can be constructed by cycles of edges created, etc. To specify the generating vertex, one or more nodes are marked with rings, meaning that the vertex is not on the mirror(s) represented by the ringed node(s). (If two or more mirrors are marked, the vertex is equidistant from them.) A mirror is active (creates reflections) only with respect to points not on it. A diagram needs at least one active node to represent a polytope.
All regular polytopes, represented by Schläfli symbol symbol {p, q, r, ...}, can have their fundamental domains represented by a set of n mirrors with a related Coxeter–Dynkin diagram of a line of nodes and branches labeled by p, q, r, ..., with the first node ringed.
Uniform polytopes with one ring correspond to generator points at the corners of the fundamental domain simplex. Two rings correspond to the edges of simplex and have a degree of freedom, with only the midpoint as the uniform solution for equal edge lengths. In general k-rings generators are on k-faces of the simplex, and if all the nodes are ringed, the generator point is in the interior of the simplex.
A secondary markup conveys a special case nonreflectional symmetry uniform polytopes. These cases exist as alternations of reflective symmetry polytopes. This markup removes the central dot of a ringed node, called a hole (circles with nodes removed), to imply alternate nodes deleted. The resulting polytope will have a subsymmetry of the original Coxeter group. If all the nodes are holes, the figure is considered a snub.
- A single node represents a single mirror. This is called group A1. If ringed this creates a line segment perpendicular to the mirror, represented as {}.
- Two unattached nodes represent two perpendicular mirrors. If both nodes are ringed, a rectangle can be created, or a square if the point is at equal distance from both mirrors.
- Two nodes attached by an order-n branch can create an n-gon if the point is on one mirror, and a 2n-gon if the point is off both mirrors. This forms the I1(n) group.
- Two parallel mirrors can represent an infinite polygon I1(∞) group, also called Ĩ1.
- Three mirrors in a triangle form images seen in a traditional kaleidoscope and can be represented by three nodes connected in a triangle. Repeating examples will have branches labeled as (3 3 3), (2 4 4), (2 3 6), although the last two can be drawn as a line (with the 2 branches ignored). These will generate uniform tilings.
- Three mirrors can generate uniform polyhedra; including rational numbers gives the set of Schwarz triangles.
- Three mirrors with one perpendicular to the other two can form the uniform prisms.
Example BC3 polytopes
For example, the BC3 Coxeter group has a diagram: . This is also called octahedral symmetry.
There are 7 convex uniform polyhedra that can be constructed from this symmetry group and 3 from its alternation subsymmetries, each with a uniquely marked up Coxeter–Dynkin diagram. The Wythoff symbol represents a special case of the Coxeter diagram for rank 3 graphs, with all 3 branch orders named, rather than suppressing the order 2 branches. The Wythoff symbol is able to handle the snub form, but not general alternations without all nodes ringed.
| Name | Cube | Truncated cube | Cuboctahedron | Truncated octahedron | Octahedron | Rhombi-cuboctahedron | Truncated cuboctahedron | Snub cube | Tetrahedron | Icosahedron |
|---|---|---|---|---|---|---|---|---|---|---|
| Image | ||||||||||
| Coxeter diagram |
||||||||||
| Wythoff symbol |
2 4 | 4 | 4 3 | 3 | 2 3 | 2 | 4 3 2 | |||
| Symmetry group | Oh | O | Td | Th | ||||||
| *432 | 432 | *332 | 3*2 | |||||||
| [4,3] | [4,3]+ | [1+,4,3] =[3,3] | [4,3+] | |||||||
Cartan matrices
Every Coxeter diagram has a corresponding Cartan matrix. All Coxeter group Cartan matrices are symmetric because their root vectors are normalized. The Cartan matrix element ai,j = aj,i = −2cos(π / p) where p is the branch order between the pairs of mirrors.
Rank 2 Coxeter diagrams and their corresponding Cartan matrices are given here. The Cartan matrices for higher rank groups can be as simply constructed with the matrix element pairs corresponding between each pair of mirrors.
The determinant the Cartan matrix determines whether a group is finite (positive), affine (zero), or hyperbolic (negative). A hyperbolic group is compact if all subgroups are finite (i.e. have positive determinants).
| Symmetry order p |
Group name |
Coxeter diagram | Cartan matrix | |||
|---|---|---|---|---|---|---|
![\left [\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/e04092cd85a8b74cac7e7e86f94a0c75.png) |
Determinant
(4-a21*a12) |
|||||
| Finite (Determinant>0) | ||||||
| 2 | I2(2) = A1xA1 | ![\left [\begin{smallmatrix}2&0\\0&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/d3483b4cea4bad9214a96818c8c94458.png) |
4 | |||
| 3 | I2(3) = A2 | ![\left [\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/13133ff56fb693a8182b3b229c32cac6.png) |
3 | |||
| 4 | I2(4) = BC2 | ![\left [\begin{smallmatrix}2&-\sqrt{2}\\-\sqrt{2}&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/69ecb148ff477cd0313d4f8c2157afcf.png) |
2 | |||
| 5 | I2(5) = H2 | ![\left [\begin{smallmatrix}2&-\phi\\-\phi&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/cf09dcddc07aa7896200ae2aa53e1b0a.png) |
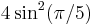
= ~1.38196601125 |
|||
| 6 | I2(6) = G2 | ![\left [\begin{smallmatrix}2&-\sqrt{3}\\-\sqrt{3}&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/efada4dc79eace7381f50899bb6104b2.png) |
1 | |||
| 8 | I2(8) | ![\left [\begin{smallmatrix}2&-2\cos(\pi/8)\\-2\cos(\pi/8)&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/38686bf9edc716f70c2c81a9d6396273.png) |
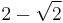 ~0.58578643763 |
|||
| 10 | I2(10) | ![\left [\begin{smallmatrix}2&-2\cos(\pi/10)\\-2\cos(\pi/10)&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/b6b5f8860b41091129b1887f519511b0.png) |
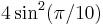
= ~0.38196601125 |
|||
| 12 | I2(12) | ![\left [\begin{smallmatrix}2&-2\cos(\pi/12)\\-2\cos(\pi/12)&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/8bedc7cf9f034a59eebff80ca9cbb7f5.png) |
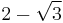 ~0.26794919243 |
|||
| p | I2(p) | ![\left [\begin{smallmatrix}2&-2\cos(\pi/p)\\-2\cos(\pi/p)&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/2e518fac12e39c570ffe7fac03776c63.png) |
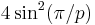 |
|||
| Affine (Determinant=0) | ||||||
| ∞ | I2(∞) = 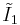 = = 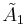 |
![\left [\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}\right ]](/2012-wikipedia_en_all_nopic_01_2012/I/b01c478b024bc2a95139bd38ae5ccf03.png) |
0 | |||
Finite Coxeter groups
- See also polytope families for a table of end-node uniform polytopes associated with these groups.
- Three different symbols are given for the same groups – as a letter/number, as a bracketed set of numbers, and as the Coxeter diagram.
- The bifurcated Dn groups is half or alternated version of the regular Cn groups.
- The bifurcated Dn and En groups are also labeled by a superscript form [3a,b,c] where a,b,c are the numbers of segments in each of the three branches.
| Rank | Simple Lie groups | Exceptional Lie groups | |||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
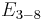 |
 / / 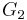 |
 |
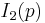 |
|
| 1 | A1=[] | ||||||
| 2 | A2=[3] | BC2=[4] | D2=A1xA1 | G2=[6] | H2=[6] | I2[p] | |
| 3 | A3=[32] | BC3=[3,4] | D3=A3 | E3=A2xA1
|
H3 | ||
| 4 | A4=[33] | BC4=[32,4] | D4=[31,1,1] | E4=A4 | F4 | H4 | |
| 5 | A5=[34] | BC5=[33,4] | D5=[32,1,1] | E5=D5 | |||
| 6 | A6=[35] | BC6=[34,4] | D6=[33,1,1] | E6=[32,2,1] | |||
| 7 | A7=[36] | BC7=[35,4] | D7=[34,1,1] | E7=[33,2,1] | |||
| 8 | A8=[37] | BC8=[36,4] | D8=[35,1,1] | E8=[34,2,1] | |||
| 9 | A9=[38] | BC9=[37,4] | D9=[36,1,1] | ||||
| 10+ | .. | .. | .. | .. | |||
Affine Coxeter groups
Families of convex uniform Euclidean tessellations are defined by the affine Coxeter groups. These groups are identical to the finite groups with the inclusion of one added node. In letter names they are given the same letter with a "~" above the letter. The index refers to the finite group, so the rank is the index plus 1. (Ernst Witt symbols for the affine groups are given as also)
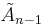 : diagrams of this type are cycles. (Also Pn)
: diagrams of this type are cycles. (Also Pn) is associated with the hypercube regular tessellation {4, 3, ...., 4} family. (Also Rn)
is associated with the hypercube regular tessellation {4, 3, ...., 4} family. (Also Rn)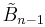 related to C by one removed mirror. (Also Sn)
related to C by one removed mirror. (Also Sn) related to C by two removed mirrors. (Also Qn)
related to C by two removed mirrors. (Also Qn)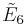 ,
, 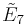 ,
, 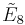 . (Also T7, T8, T9)
. (Also T7, T8, T9)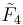 forms the {3,4,3,3} regular tessellation. (Also U5)
forms the {3,4,3,3} regular tessellation. (Also U5)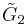 forms 30-60-90 triangle fundamental domains. (Also V3)
forms 30-60-90 triangle fundamental domains. (Also V3)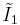 is two parallel mirrors. ( =
is two parallel mirrors. ( = 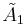 =
= 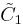 ) (Also W2)
) (Also W2)
| Rank | 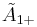 (P2+) (P2+) |
 (S4+) (S4+) |
 (R2+) (R2+) |
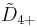 (Q5+) (Q5+) |
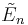 (Tn+1) / (Tn+1) / 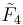 (U5) / (U5) / 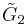 (V3) (V3) |
|---|---|---|---|---|---|
| 2 | 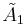 =[∞] =[∞] |
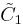 =[∞] =[∞] |
|||
| 3 |  =[3[3]] =[3[3]] |
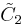 =[4,4] =[4,4] |
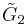 =[6,3] =[6,3] |
||
| 4 | 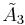 =[3[4]] =[3[4]] |
 =[4,31,1] =[4,31,1] |
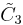 =[4,3,4] =[4,3,4] |
||
| 5 | 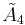 =[3[5]] =[3[5]] |
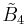 =[4,3,31,1] =[4,3,31,1] |
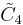 =[4,32,4] =[4,32,4] |
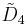 =[31,1,1,1] =[31,1,1,1] |
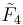 =[3,4,3,3] =[3,4,3,3] |
| 6 |  =[3[6]] =[3[6]] |
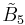 =[4,32,31,1] =[4,32,31,1] |
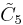 =[4,33,4] =[4,33,4] |
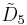 =[31,1,3,31,1] =[31,1,3,31,1] |
|
| 7 |  =[3[7]] =[3[7]] |
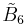 =[4,33,31,1] =[4,33,31,1] |
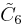 =[4,34,4] =[4,34,4] |
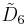 =[31,1,32,31,1] =[31,1,32,31,1] |
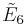 =[32,2,2] =[32,2,2] |
| 8 |  =[3[8]] =[3[8]] |
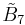 =[4,34,31,1] =[4,34,31,1] |
 =[4,35,4] =[4,35,4] |
 =[31,1,33,31,1] =[31,1,33,31,1] |
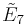 =[33,3,1] =[33,3,1] |
| 9 | 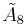 =[3[9]] =[3[9]] |
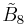 =[4,35,31,1] =[4,35,31,1] |
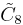 =[4,36,4] =[4,36,4] |
 =[31,1,34,31,1] =[31,1,34,31,1] |
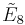 =[35,2,1] =[35,2,1] |
| 10 | 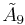 =[3[10]] =[3[10]] |
 =[4,36,31,1] =[4,36,31,1] |
 =[4,37,4] =[4,37,4] |
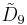 =[31,1,35,31,1] =[31,1,35,31,1] |
|
| 11 | ... | ... | ... | ... |
Hyperbolic Coxeter groups
There are many infinite hyperbolic Coxeter groups. Hyperbolic groups are categorized as compact or not, with compact groups having bounded fundamental domains. Compact hyperbolic groups exist of rank 3 to 5, and noncompact groups exist up to rank 10.
Compact
Rank 3
There are infinitely many compact hyperbolic Coxeter groups of rank 3, including linear and triangle graphs. See notably the hyperbolic triangle groups.[2]
| Linear | Cyclic | ||||
|---|---|---|---|---|---|
| ∞ [p,q], : 2(p+q)<pq
|
∞ [(p,q,r)], : p+q+r>9
|
Ranks 4–5
The fundamental domain of either of the two bifurcating groups, [5,31,1] and [5,3,31,1], is double that of a corresponding linear group, [5,3,4] and [5,3,3,4] respectively. Letter names are given by Johnson as extended Witt symbols.[3]
| Dimension Hd |
Rank | Total count | Linear | Bifurcating | Cyclic |
|---|---|---|---|---|---|
| H3 | 4 | 9 |
|
|
|
| H4 | 5 | 5 |
|
|
|
Noncompact
The highest noncompact hyperbolic Coxeter group is rank 10.
Rank 3
Noncompact Coxeter groups of rank 3 include linear and triangle graphs with one or more infinite order branches: (p and q = 3,4,5...)
| Linear graphs | Cyclic graphs |
|---|---|
|
|
Ranks 4–10
There are a total of 58 noncompact hyperbolic Coxeter groups from rank 4 through 10. All 58 are grouped below in five categories. Letter symbols are given by Johnson as Extended Witt symbols, using PQRSTWUV from the affine Witt symbols, and adding LMNOXYZ. These hyperbolic groups are given an overline, or a hat, for purely cyclic graphs. The bracket notation from Coxeter is a linearized representation of the Coxeter group.
| Rank | Total count |
Groups | |||
|---|---|---|---|---|---|
| 4 | 23 |
|
|
|
|
| 5 | 9 | 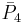 = [3,3[4]]: = [3,3[4]]:
|
|
|
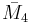 = [4,31,1,1]: = [4,31,1,1]: |
| 6 | 12 |
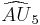 = [(3,3,3,3,3,4)]: = [(3,3,3,3,3,4)]:
|
|
|
 = [32,1,1,1]: = [32,1,1,1]:
|
| 7 | 3 |
|
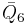 = [31,1,3,32,1]: = [31,1,3,32,1]: |
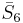 = [4,3,3,32,1]: = [4,3,3,32,1]: |
|
| 8 | 4 | 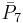 = [3,3[7]]: = [3,3[7]]: |
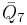 = [31,1,32,32,1]: = [31,1,32,32,1]: |
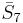 = [4,33,32,1]: = [4,33,32,1]: |
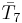 = [33,2,2]: = [33,2,2]: |
| 9 | 4 | 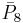 = [3,3[8]]: = [3,3[8]]: |
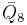 = [31,1,33,32,1]: = [31,1,33,32,1]: |
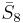 = [4,34,32,1]: = [4,34,32,1]: |
 = [34,3,1]: = [34,3,1]: |
| 10 | 3 |  = [31,1,34,32,1]: = [31,1,34,32,1]: |
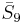 = [4,35,32,1]: = [4,35,32,1]: |
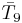 = [36,2,1]: = [36,2,1]: |
|
Lorentzian groups
Coxeter groups can be defined as graphs beyond the hyperbolic forms. These can be considered to be related to a Lorentzian geometry, named after Hendrik Lorentz in the field of special and general relativity space-time, containing one (or more) time-like dimensional components whose self dot products are negative.[3]
One usage includes the "very-extended" definitions which adds a third node to the over-extended simple groups. See family En (Lie algebra) with E11 as a very-extended Coxeter–Dynkin diagram.
Geometric folding
Finite |
Affine |
Hyperbolic |
A (simply-laced) Coxeter–Dynkin diagram (finite or affine) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called "folding".[4]
The one condition on the automorphism for folding to be possible is that distinct nodes of the graph in the same orbit (under the automorphism) must not be connected by an edge; at the level of root systems, roots in the same orbit must be orthogonal.[5] At the level of diagrams, this is necessary as otherwise the quotient diagram will have a loop, due to identifying two nodes but having an edge between them, and loops are not allowed in Coxeter–Dynkin diagrams.
The nodes and edges of the quotient ("folded") diagram are the orbits of nodes and edges of the original diagram; the edges are single unless two incident edges map to the same edge (notably at nodes of valence greater than 2) – a "branch point" of the map, in which case the weight is the number of incident edges, and the arrow points towards the node at which they are incident – "the branch point maps to the non-homogeneous point".
For example, in D4 folding to G2, the edge in G2 points from the class of the 3 outer nodes (valence 1), to the class of the central node (valence 3).
Geometrically this corresponds to orthogonal projections of uniform polytopes. Notably, any finite simply-laced Coxeter–Dynkin diagram can be folded to I2(h), where h is the Coxeter number, which corresponds geometrically to a projection to the Coxeter plane.
See also
Notes
- ^ Hall, Brian C. (2003), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 0-387-40122-9
- ^ The Geometry and Topology of Coxeter Groups, Michael W. Davis, 2008 p. 105 Table 6.2. Hyperbolic diagrams
- ^ a b Norman Johnson, Geometries and Transformations, Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices
- ^ Generalized Dynkin diagrams and root systems and their folding by Jean-Bernard Zuber, pp. 28–30
- ^ Folding by Automorphisms, John Stembridge, 4pp., 79K, 20 August 2008, Other Articles by John Stembridge
References
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1], Googlebooks [2]
- (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Coxeter, Regular Polytopes (1963), Macmillian Company
- Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
- Norman Johnson, Geometries and Transformations, Chapters 11,12,13, preprint 2011
External links
- Weisstein, Eric W., "Coxeter–Dynkin diagram" from MathWorld.
- October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Cornell University Library.
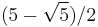

 = [4,3,5]:
= [4,3,5]: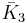 = [5,3,5]:
= [5,3,5]: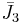 = [3,5,3]:
= [3,5,3]: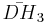 = [5,31,1]:
= [5,31,1]: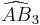 = [(3,3,3,4)]:
= [(3,3,3,4)]: 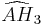 = [(3,3,3,5)]:
= [(3,3,3,5)]: 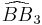 = [(3,4,3,4)]:
= [(3,4,3,4)]: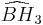 = [(3,4,3,5)]:
= [(3,4,3,5)]: = [(3,5,3,5)]:
= [(3,5,3,5)]: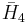 = [3,3,3,5]:
= [3,3,3,5]: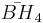 = [4,3,3,5]:
= [4,3,3,5]: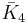 = [5,3,3,5]:
= [5,3,3,5]: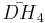 = [5,3,31,1]:
= [5,3,31,1]: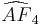 = [(3,3,3,3,4)]:
= [(3,3,3,3,4)]: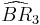 = [(3,3,4,4)]:
= [(3,3,4,4)]: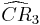 = [(3,4,4,4)]:
= [(3,4,4,4)]: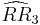 = [4[4]]:
= [4[4]]: = [(3,3,3,6)]:
= [(3,3,3,6)]: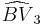 = [(3,4,3,6)]:
= [(3,4,3,6)]: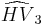 = [(3,5,3,6)]:
= [(3,5,3,6)]: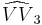 = [(3,6,3,6)]:
= [(3,6,3,6)]: = [3,3[3]]:
= [3,3[3]]: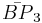 = [4,3[3]]:
= [4,3[3]]: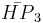 = [5,3[3]]:
= [5,3[3]]: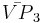 = [6,3[3]]:
= [6,3[3]]: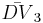 = [6,31,1]:
= [6,31,1]: = [3,41,1]:
= [3,41,1]: = [41,1,1]:
= [41,1,1]: = [3,4,4]:
= [3,4,4]: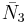 = [4,4,4]:
= [4,4,4]: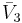 = [3,3,6]:
= [3,3,6]: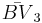 = [4,3,6]:
= [4,3,6]: = [5,3,6]:
= [5,3,6]: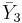 = [3,6,3]:
= [3,6,3]: = [6,3,6]:
= [6,3,6]: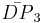 = [3[ ]x[ ]]:
= [3[ ]x[ ]]: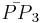 = [3[3,3]]:
= [3[3,3]]: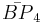 = [4,3[4]]:
= [4,3[4]]: = [(3,3,4,3,4)]:
= [(3,3,4,3,4)]: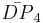 = [3[3]x[ ]]:
= [3[3]x[ ]]: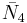 = [4,/3\,3,4]:
= [4,/3\,3,4]: = [3,4,31,1]:
= [3,4,31,1]: = [4,32,1]:
= [4,32,1]: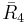 = [3,4,3,4]:
= [3,4,3,4]: = [3,3[5]]:
= [3,3[5]]: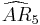 = [(3,3,4,3,3,4)]:
= [(3,3,4,3,3,4)]: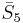 = [4,3,32,1]:
= [4,3,32,1]: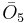 = [3,4,31,1]:
= [3,4,31,1]: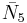 = [4,3,/3\,3,4]:
= [4,3,/3\,3,4]: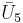 = [3,3,3,4,3]:
= [3,3,3,4,3]: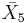 = [3,3,4,3,3]:
= [3,3,4,3,3]: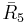 = [3,4,3,3,4]:
= [3,4,3,3,4]: = [4,3,31,1,1]:
= [4,3,31,1,1]: = [31,1,1,1,1]:
= [31,1,1,1,1]: = [3,3[6]]:
= [3,3[6]]: